- Paraboloïde elliptique
-
● Paraboloïde elliptique quadrique d'équation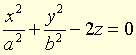 .
.
Encyclopédie Universelle. 2012.
● Paraboloïde elliptique quadrique d'équation
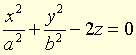 .
.Encyclopédie Universelle. 2012.
Paraboloïde elliptique — Paraboloïde En mathématiques, un paraboloïde est une surface du second degré de l espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de ne pas posséder de centre de symétrie. Certaines sections d un… … Wikipédia en Français
paraboloïde — [ parabɔlɔid ] n. m. • 1691; adj. 1660 ; de 2. parabole ♦ Géom. Quadrique n ayant pas de centre. Paraboloïde elliptique, hyperbolique, dont certaines sections planes sont des ellipses, des hyperboles. Paraboloïde de révolution : surface engendrée … Encyclopédie Universelle
Paraboloide — Paraboloïde En mathématiques, un paraboloïde est une surface du second degré de l espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de ne pas posséder de centre de symétrie. Certaines sections d un… … Wikipédia en Français
Paraboloïde circulaire — Paraboloïde En mathématiques, un paraboloïde est une surface du second degré de l espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de ne pas posséder de centre de symétrie. Certaines sections d un… … Wikipédia en Français
Paraboloïde hyperbolique — Paraboloïde En mathématiques, un paraboloïde est une surface du second degré de l espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de ne pas posséder de centre de symétrie. Certaines sections d un… … Wikipédia en Français
Paraboloïde de révolution — ● Paraboloïde de révolution paraboloïde elliptique particulier, obtenu quand a = b … Encyclopédie Universelle
Paraboloïde — En mathématiques, un paraboloïde est une surface du second degré de l espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de ne pas posséder de centre de symétrie. Certaines sections d un paraboloïde avec un … Wikipédia en Français
paraboloïde — (pa ra bo lo i d ) s. m. 1° Terme de géométrie. Surface du deuxième degré dépourvue de centre. On distingue deux sortes de paraboloïdes : le paraboloïde elliptique, qui est composé d une seule nappe infinie ; et le paraboloïde hyperbolique qui… … Dictionnaire de la Langue Française d'Émile Littré
elliptique — 1. elliptique [ eliptik ] adj. • 1655; gr. elleiptikos → 1. ellipse ♦ Qui présente une ellipse, des ellipses (1.). Construction, proposition elliptique. Style elliptique. ⇒ télégraphique. Par ext. Qui fait des ellipses, ne développe pas sa pensée … Encyclopédie Universelle
Quadrique — En mathématiques, et plus précisément en géométrie euclidienne, une quadrique, ou surface quadratique, est une surface de l espace euclidien de dimension 3, lieu des points vérifiant une équation cartésienne de degré 2 Ax2 + By2 + Cz2 + 2Dyz +… … Wikipédia en Français